A análise combinatória ou combinatória são cálculos que permitem a formação de grupos relacionados à contagem.
Faz análise das possibilidades e das combinações possíveis entre um conjunto de elementos. Por isso, é muito utilizada nos estudos sobre probabilidade e lógica.
Probabilidade
A Probabilidade é um conceito da matemática que permite analisar ou calcular as chances de obter determinado resultado diante de um experimento aleatório. São exemplos um lançamento de dados ou a possibilidade de ganhar na loteria.
A partir disso, a probabilidade determina o resultado entre o número de eventos possíveis e número de eventos favoráveis, apresentada pela seguinte expressão:
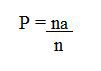
Donde
P: probabilidade
na: número de casos (eventos) favoráveis
n: número de casos (eventos) possíveis
na: número de casos (eventos) favoráveis
n: número de casos (eventos) possíveis
Princípio Fundamental da Contagem
O princípio fundamental da contagem postula que:
“quando um evento é composto por n etapas sucessivas e independentes, de tal modo que as possibilidades da primeira etapa é x e as possibilidades da segunda etapa é y, resulta no número total de possibilidades de o evento ocorrer, dado pelo produto (x) . (y)”.
Em resumo, no princípio fundamental da contagem, multiplica-se o número de opções entre as escolhas que lhe são apresentadas.
Como exemplo, podemos pensar na combinação de roupas de uma garota, sendo que ela possui 3 tipos de calças, 4 tipos de blusas, 2 tipos de sapatos e 3 tipos de bolsas.
Logo, para saber quais as diferentes possibilidades que a garota possui basta multiplicar o número de peças: 3 x 4 x 2 x 3 = 72.
Portanto, a garota possui 72 possibilidades de configurações diferentes para o uso das peças de roupas e dos acessórios apresentados.
Tipos de Combinatória
A combinatória utiliza de importantes ferramentas, ou seja, há três tipos básicos de agrupamento dos elementos: arranjos, combinações e permutações. Todas utilizam o fatorial:
Arranjos
Nos arranjos, os agrupamentos dos elementos dependem da ordem e da natureza dos mesmos.
Para obter o arranjo simples de n elementos tomados, p a p (p ≤ n), utiliza-se a seguinte expressão:
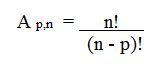
Como exemplo de arranjo, podemos pensar nas eleições, de modo que 20 deputados concorrem a 2 vagas no estado de São Paulo.
Dessa forma, de quantas maneiras distintas a escolha poderá ser feita? Observe que nesse caso, a ordem é importante, visto que altera o resultado final.
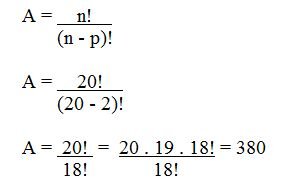
Logo, o arranjo pode ser feito de 380 maneiras diferentes.
Combinações
As combinações são subconjuntos em que a ordem dos elementos não é importante, entretanto, são caracterizadas pela natureza dos mesmos.
Assim, para calcular uma combinação simples de n elementos tomados p a p (p ≤ n), utiliza-se a seguinte expressão:
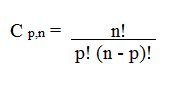
A fim de exemplificar, podemos pensar na escolha de 3 membros para formar a comissão organizadora de um evento, dentre as 10 pessoas que se candidataram.
Para tanto, Maria, João e José são os escolhidos. De quantas maneiras distintas esse grupo pode se combinar?
Note que, ao contrário dos arranjos, nas combinações a ordem dos elementos não é relevante. Isso quer dizer que a combinação Maria, João e José é equivalente à João, José e Maria.
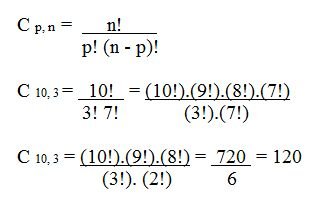
Logo, há 120 maneiras distintas de combinar os 3 membros da comissão.
Permutações
As permutações são agrupamentos ordenados, donde o número de elementos (n) do agrupamento é igual ao número de elementos disponíveis, expresso pela fórmula:
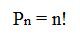
Para exemplificar, pensemos de quantas maneiras diferentes poderiam surgir a sequência de resultados dos 5 números que saíram na loteria: 11, 12, 44, 52, 61.
Sendo assim, os números que compõem o resultado final é uma sequência de 6 números, logo:
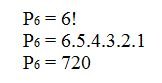
Logo, o resultado final da loteria, podem ser permutados 720 vezes.