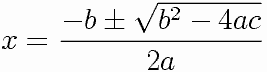GEOMETRIA ANALÍTICA

Em uma matriz, os elementos estão dispostos em linhas e colunas.

Para representar matrizes, utilizamos a disposição de uma tabela. Chamamos de matriz toda a tabela m x n ( lê-se “m por n”) em que números estão dispostos em linhas (m) e colunas (n). Cada elemento da matriz é indicado por a_ii (i indica a posição do elemento referente à linha, e j, a posição em relação à coluna). Acompanhe a seguir a representação de uma matriz m x n.

Nessa matriz, temos que:

a_ij→ linha (i) e coluna (j)

a_1,1→ linha 1 e coluna 1
a_1,2 → linha 1 e coluna 2
a_1,3 → linha 1 e coluna 3
a_1,n → linha 1 e coluna n

a_2,1 → linha 2 e coluna 1
a_2,2 → linha 2 e coluna 2
a_2,3→ linha 2 e coluna 3
a_2,n → linha 2 e coluna n

a_m,1→ linha m e coluna 1
a_m,2→ linha m e coluna 2
a_m,3→ linha m e coluna 3
a_m,n→ linha m e coluna n

Diagonais da Matriz

Toda matriz possui diagonal principal e diagonal secundária. A diagonal principal é formada pelos elementos em que i = j. A diagonal secundária é composta por elementos em que a soma de i com j sempre resulta em uma mesma solução. Veja como identificamos as diagonais de uma matriz:

Diagonal Principal

a_1,1→ linha 1 e coluna 1
a_2,2→ linha 2 e coluna 2
a_3,3→ linha 3 e coluna 3

Diagonal Secundária

a_1,3→ linha 1 + coluna 3 = 4
a_2,2→ linha 2 + coluna 2 = 4
a_3,1→ linha 3 + coluna 1 = 4

Matrizes Especiais

Existem algumas matrizes que são consideradas especiais pela forma como são organizadas. Entre essas matrizes, podemos destacar:

Matriz quadrada: é toda a matriz em que o número de linhas é igual ao número de colunas. Exemplos:

Observe que a matriz acima apresenta três linhas e três colunas. Como o número de linhas é igual ao de colunas, a matriz é quadrada.

Matriz identidade: todos os elementos da diagonal principal são iguais a 1, e os demais números são iguais a zero.

Matriz nula: é toda matriz em que seus elementos são iguais a zero.

Matriz linha: é formada por uma única linha.

Matriz coluna: é formada por uma única coluna.

Operações com matrizes

As operações com matrizes são: adição, subtração e multiplicação.

Adição: Sejam A e B duas matrizes em que a sua soma resulta em uma matriz C.

A + B = C

Cada um dos elementos da matriz C é o resultado da soma de um elemento de A com um elemento de B. Para efetuarmos a adição entre duas matrizes, elas devem possuir o mesmo número de linhas e colunas. Acompanhe o exemplo abaixo:

A + B = C
A_{2 x 3}+ B_{2 x 3}= C_{2 x 3}

Observe que as matrizes A e B possuem a mesma quantidade de linhas (m = 2) e a mesma quantidade de colunas (n = 3). A matriz C é resultante da soma de A + B e também deve possuir duas linhas e três colunas.

Subtração: A partir de duas matrizes A e B, definimos a sua diferença como C:

A – B =C
A + (- B) = C

A matriz diferença pode ser definida como sendo a soma de A com o oposto de B, ou seja, - B. Para realizarmos a subtração entre duas matrizes, elas devem possuir o mesmo número de linhas e colunas. Acompanhe o exemplo abaixo e verifique como é feita a subtração entre duas matrizes:

Multiplicação: Dadas as matrizes A_{m x n}e B_{n x p}, para que seja possível realizar o seu produto, o número de colunas da matriz A deve ser igual ao número de linhas da matriz B. Esse processo resulta em uma matriz C_{m x p.} Observe o exemplo abaixo e veja como isso é feito:

Descrição dos elementos da matriz:

a_1,₁ → Produto dos elementos da linha 1 da matriz A com os elementos da coluna 1 da matriz B.

a_1,₂ → Produto dos elementos da linha 1 da matriz A com os elementos da coluna 2 da matriz B.

a_1,₃ → Produto dos elementos da linha 1 da matriz A com os elementos da coluna 3 da matriz B.

a_2,₁ → Produto dos elementos da linha 2 da matriz A com os elementos da coluna 1 da matriz B.

a_2,₂ → Produto dos elementos da linha 2 da matriz A com os elementos da coluna 2 da matriz B.

a_2,₃ → Produto dos elementos da linha 2 da matriz A com os elementos da coluna 3 da matriz B.

Determinante

Calculamos o determinante de matrizes quadradas, isto é, aquelas em que o número de linhas é igual ao número de colunas. Observe:

Definimos como determinante da matriz A (det A) o número que é obtido pela operação dos elementos que compõem A.

Caso A possua uma linha e uma coluna (A_{1 X 1}), então o determinante será representado pelo único elemento que compõe A. Exemplo:

A = (10)
det A = 10
Se A possuir duas linhas e colunas (A_{2 x 2}), então o determinante (det A_{2 x 2}) será dado pela diferença entre os produtos da diagonal principal da matriz A pelo produto dos elementos que compõem a sua diagonal secundária. Veja abaixo como é feito o cálculo do determinante de uma matriz 2 por 2 (A _{2 X 2}).

Para toda matriz quadrada 2 por 2, o cálculo do determinante é realizado da forma como está demonstrado acima. Caso a matriz quadrada seja do tipo M _{3 X 3}, M _{4 X 4}, M _{5 X 5}e assim por diante, calculamos o seu determinante executando os passos descritos abaixo:

Faça o espelhamento da primeira e da segunda coluna da matriz, ou seja, repita a primeira e a segunda coluna;
Realize os produtos de cada diagonal principal e secundária separadamente;
Efetue a soma entre os termos obtidos dos produtos de cada diagonal;
Realize a diferença entre os resultados obtidos referente à soma dos termos das diagonais principais e das secundárias. No fim desses cálculos, teremos o determinante da matriz.

det M_{3 X 3} = a _1,1 . a _2,2 . a _3,3+ a _1,2 + a _1,2 . a _2,3 . a _3,1 + a _1,3 . a _2,1 . a _3,2 - ( a _1,3 . a _2,2. a _3,1 + a _1,1 . a _2,3 . a _3,2 + a _1,2 . a _2,1 . a _3,3).

A análise combinatória ou combinatória são cálculos que permitem a formação de grupos relacionados à contagem.

Faz análise das possibilidades e das combinações possíveis entre um conjunto de elementos. Por isso, é muito utilizada nos estudos sobre probabilidade e lógica.

Probabilidade

A Probabilidade é um conceito da matemática que permite analisar ou calcular as chances de obter determinado resultado diante de um experimento aleatório. São exemplos um lançamento de dados ou a possibilidade de ganhar na loteria.

A partir disso, a probabilidade determina o resultado entre o número de eventos possíveis e número de eventos favoráveis, apresentada pela seguinte expressão:

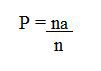
Donde

P: probabilidade
na: número de casos (eventos) favoráveis
n: número de casos (eventos) possíveis

Princípio Fundamental da Contagem

O princípio fundamental da contagem postula que:

“quando um evento é composto por n etapas sucessivas e independentes, de tal modo que as possibilidades da primeira etapa é x e as possibilidades da segunda etapa é y, resulta no número total de possibilidades de o evento ocorrer, dado pelo produto (x) . (y)”.

Em resumo, no princípio fundamental da contagem, multiplica-se o número de opções entre as escolhas que lhe são apresentadas.

Como exemplo, podemos pensar na combinação de roupas de uma garota, sendo que ela possui 3 tipos de calças, 4 tipos de blusas, 2 tipos de sapatos e 3 tipos de bolsas.

Logo, para saber quais as diferentes possibilidades que a garota possui basta multiplicar o número de peças: 3 x 4 x 2 x 3 = 72.

Portanto, a garota possui 72 possibilidades de configurações diferentes para o uso das peças de roupas e dos acessórios apresentados.

Tipos de Combinatória

A combinatória utiliza de importantes ferramentas, ou seja, há três tipos básicos de agrupamento dos elementos: arranjos, combinações e permutações. Todas utilizam o fatorial:

Arranjos

Nos arranjos, os agrupamentos dos elementos dependem da ordem e da natureza dos mesmos.

Para obter o arranjo simples de n elementos tomados, p a p (p ≤ n), utiliza-se a seguinte expressão:

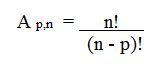
Como exemplo de arranjo, podemos pensar nas eleições, de modo que 20 deputados concorrem a 2 vagas no estado de São Paulo.

Dessa forma, de quantas maneiras distintas a escolha poderá ser feita? Observe que nesse caso, a ordem é importante, visto que altera o resultado final.

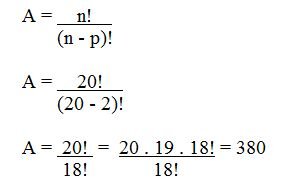
Logo, o arranjo pode ser feito de 380 maneiras diferentes.

Combinações

As combinações são subconjuntos em que a ordem dos elementos não é importante, entretanto, são caracterizadas pela natureza dos mesmos.

Assim, para calcular uma combinação simples de n elementos tomados p a p (p ≤ n), utiliza-se a seguinte expressão:

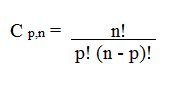
A fim de exemplificar, podemos pensar na escolha de 3 membros para formar a comissão organizadora de um evento, dentre as 10 pessoas que se candidataram.

Para tanto, Maria, João e José são os escolhidos. De quantas maneiras distintas esse grupo pode se combinar?

Note que, ao contrário dos arranjos, nas combinações a ordem dos elementos não é relevante. Isso quer dizer que a combinação Maria, João e José é equivalente à João, José e Maria.

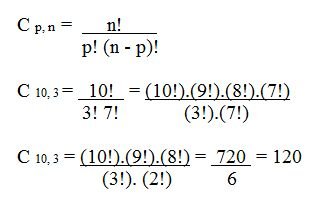
Logo, há 120 maneiras distintas de combinar os 3 membros da comissão.

Permutações

As permutações são agrupamentos ordenados, donde o número de elementos (n) do agrupamento é igual ao número de elementos disponíveis, expresso pela fórmula:

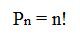
Para exemplificar, pensemos de quantas maneiras diferentes poderiam surgir a sequência de resultados dos 5 números que saíram na loteria: 11, 12, 44, 52, 61.

Sendo assim, os números que compõem o resultado final é uma sequência de 6 números, logo:

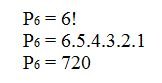
Logo, o resultado final da loteria, podem ser permutados 720 vezes.

Introdução às equações algébricas

Equações algébricas são equações nas quais a incógnita x está sujeita a operações algébricas como: adição, subtração, multiplicação, divisão e radiciação.

Exemplos:

a x + b = 0
a x² + bx + c = 0
a x4 + b x² + c = 0

Uma equação algébrica está em sua forma canônica, quando ela pode ser escrita como:

ao xn + a1 xn-1 + ... + an-1 x1 + an = 0

onde n é um número inteiro positivo (número natural). O maior expoente da incógnita em uma equação algébrica é denominado o grau da equação e o coeficiente do termo de mais alto grau é denominado coeficiente do termo dominante.

Exemplo: A equação 4x²+3x+2=0 tem o grau 2 e o coeficiente do termo dominante é 4. Neste caso, dizemos que esta é uma equação do segundo grau.

A fórmula quadrática de Sridhara (Bhaskara)

Mostraremos na sequência como o matemático Sridhara, obteve a Fórmula (conhecida como sendo) de Bhaskara, que é a fórmula geral para a resolução de equações do segundo grau. Um fato curioso é que a Fórmula de Bhaskara não foi descoberta por ele mas pelo matemático hindu Sridhara, pelo menos um século antes da publicação de Bhaskara, fato reconhecido pelo próprio Bhaskara, embora o material construído pelo pioneiro não tenha chegado até nós.

O fundamento usado para obter esta fórmula foi buscar uma forma de reduzir a equação do segundo grau a uma do primeiro grau, através da extração de raízes quadradas de ambos os membros da mesma.

Seja a equação:

a x² + b x + c = 0

com a não nulo e dividindo todos os coeficientes por a, temos:

x² + (b/a) x + c/a = 0

Passando o termo constante para o segundo membro, teremos:

x² + (b/a) x = -c/a

Prosseguindo, faremos com que o lado esquerdo da equação seja um quadrado perfeito e para isto somaremos o quadrado de b/2a a ambos os membros da equação para obter:

x² + (b/a) x + (b/2a)² = -c/a + (b/2a)²

Simplificando ambos os lados da equação, obteremos:

[x+(b/2a)]2 = (b² - 4ac) / 4a²

Notação: Usaremos a notação R[x] para representar a raiz quadrada de x>0. R[5] representará a raiz quadrada de 5. Esta notação está sendo introduzida aqui para fazer com que a página seja carregada mais rapidamente, pois a linguagem HTML ainda não permite apresentar notações matemáticas na Internet de uma forma fácil.

Extraindo a raiz quadrada de cada membro da equação e lembrando que a raiz quadrada de todo número real não negativo é também não negativa, obteremos duas respostas para a nossa equação:

x + (b/2a) = + R[(b²-4ac) / 4a²]

x + (b/2a) = - R[(b²-4ac) / 4a²]

que alguns, por preguiça ou descuido, escrevem:

contendo um sinal ± que é lido como mais ou menos. Lembramos que este sinal ± não tem qualquer significado em Matemática.

Como estamos procurando duas raízes para a equação do segundo grau, deveremos sempre escrever:

x' = -b/2a + R[b²-4ac] /2a

x" = -b/2a - R[b²-4ac] /2a

A fórmula de Bhaskara ainda pode ser escrita como:

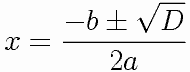
onde D (às vezes usamos a letra maiúscula "delta" do alfabeto grego) é o discriminante da equação do segundo grau, definido por:

D = b² - 4ac

Equação do segundo grau

Uma equação do segundo grau na incógnita x é da forma:

a x² + b x + c = 0

onde os números reais a, b e c são os coeficientes da equação, sendo que a deve ser diferente de zero. Essa equação é também chamada de equação quadrática, pois o termo de maior grau está elevado ao quadrado.

Equação Completa do segundo grau

Uma equação do segundo grau é completa, se todos os coeficientes a, b e c são diferentes de zero.

Exemplos:

2 x² + 7x + 5 = 0
3 x² + x + 2 = 0

Equação incompleta do segundo grau

Uma equação do segundo grau é incompleta se b=0 ou c=0 ou b=c=0. Na equação incompleta o coeficiente a é diferente de zero.

Exemplos:

4 x² + 6x = 0
3 x² + 9 = 0
2 x² = 0

Resolução de equações incompletas do 2o. grau

Equações do tipo ax²=0: Basta dividir toda a equação por a para obter:

x² = 0

significando que a equação possui duas raízes iguais a zero.

Equações do tipo ax²+c=0: Novamente dividimos toda a equação por a e passamos o termo constante para o segundo membro para obter:

x² = -c/a

Se -c/a for negativo, não existe solução no conjunto dos números reais.

Se -c/a for positivo, a equação terá duas raízes com o mesmo valor absoluto (módulo) mas de sinais contrários.

Equações do tipo ax²+bx=0: Neste caso, fatoramos a equação para obter:

x (ax + b) = 0

e a equação terá duas raízes:

x' = 0 ou x" = -b/a

Exemplos gerais

4x²=0 tem duas raízes nulas.
4x²-8=0 tem duas raízes: x'=R[2], x"= -R[2]
4x²+5=0 não tem raízes reais.
4x²-12x=0 tem duas raízes reais: x'=3, x"=0

Exercícios: Resolver as equações incompletas do segundo grau.

x² + 6x = 0
2 x² = 0
3 x² + 7 = 0
2 x² + 5 = 0
10 x² = 0
9 x² - 18 = 0

Resolução de equações completas do 2o. grau

Como vimos, uma equação do tipo: ax²+bx+c=0, é uma equação completa do segundo grau e para resolvê-la basta usar a fórmula quadrática (atribuída a Bhaskara), que pode ser escrita na forma:

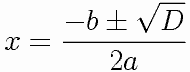
onde D=b²-4ac é o discriminante da equação.

Para esse discriminante D há três possíveis situações:

Se D<0, não há solução real, pois não existe raiz quadrada real de número negativo.
Se D=0, há duas soluções iguais:
x' = x" = -b / 2a
Se D>0, há duas soluções reais e diferentes:
x' = (-b + R[D])/2a
x" = (-b - R[D])/2a

Exemplos: Preencher a tabela com os coeficientes e o discriminante de cada equação do segundo grau, analisando os tipos de raízes da equação.

Equação	a	b	c	Delta	Tipos de raízes
x²-6x+8=0	1	-6	8	4	reais e diferentes
x²-10x+25=0
x²+2x+7=0
x²+2x+1=0
x²+2x=0

O uso da fórmula de Bhaskara

Você pode realizar o Cálculo das Raízes da Equação do segundo grau com a entrada dos coeficientes a, b e c em um formulário, mesmo no caso em que D é negativo, o que força a existência de raízes complexas conjugadas. Para estudar estas raízes, visite o nosso link Números Complexos.

Mostraremos agora como usar a fórmula de Bhaskara para resolver a equação:

x² - 5 x + 6 = 0

Identificar os coeficientes: a=1, b= -5, c=6
Escrever o discriminante D = b²-4ac.
Calcular D=(-5)²-4×1×6=25-24=1
Escrever a fórmula de Bhaskara:
Substituir os valores dos coeficientes a, b e c na fórmula:
x' = (1/2)(5+R[1]) = (5+1)/2 = 3
x" = (1/2)(5-R[1]) = (5-1)/2 = 2

Exercícios

Calcular o discriminante de cada equação e analisar as raízes em cada caso:
1. x² + 9 x + 8 = 0
2. 9 x² - 24 x + 16 = 0
3. x² - 2 x + 4 = 0
4. 3 x² - 15 x + 12 = 0
5. 10 x² + 72 x - 64 = 0
Resolver as equações:
1. x² + 6 x + 9 = 0
2. 3 x² - x + 3 = 0
3. 2 x² - 2 x - 12 = 0
4. 3 x² - 10 x + 3 = 0

Equações fracionárias do segundo grau

São equações do segundo grau com a incógnita aparecendo no denominador.

Exemplos:

3/(x² - 4) + 1/(x - 3) = 0
3/(x²-4)+1/(x-2)=0

Para resolver este tipo de equação, primeiramente devemos eliminar os valores de x que anulam os denominadores, uma vez que tais valores não servirão para as raízes da equação, pois não existe fração com denominador igual a 0. Na sequência extraímos o mínimo múltiplo comum de todos os termos dos denominadores das frações, se houver necessidade.

Consideremos o primeiro exemplo:
3/(x² - 4) + 1/(x - 3) = 0

x deve ser diferente de 3, diferente de 2 e diferente de -2, assim podemos obter o mínimo múltiplo comum entre os termos como:

MMC(x) = (x² - 4)(x - 3)

Reduzindo as frações ao mesmo denominador que deverá ser MMC(x), teremos:

[3(x-3) + 1(x²-4)] / (x²-4)(x-3) = 0

o que significa que o numerador deverá ser:

3(x - 3) + 1(x² - 4) = 0

que desenvolvido nos dá:

x2 + 3x - 13 = 0

que é uma equação do segundo grau que pode ser resolvida pela fórmula de Bhaskara. Não existirão números reais satisfazendo esta equação.
Consideremos agora o segundo exemplo:
(x+3)/(2x-1)=2x/(x+4)

O mínimo múltiplo comum entre 2x-1 e x+4 é MMC=(2x-1)(x-4) (o produto entre estes fatores) e MMC somente se anulará se x=1/2 ou x= -4. Multiplicando os termos da equação pelo MMC, teremos uma sequência de expressões como:
```
                                    (x+3)(x+4)=2x(2x-1)x² + 7x + 12 = 4x² - 2x-3x² + 9x + 12 = 03x² - 9x - 12 = 0x² - 3x - 4 = 0(x-4)(x+1) = 0

                                                
            
```
Solução: x'=4 ou x"= -1
Estudemos outro exemplo:
3/(x²-4)+1/(x-2)=0

O mínimo múltiplo comum é MMC=x²-4=(x-2)(x+2) e este MMC somente se anulará se x=2 ou x= -2. Multiplicando os termos da equação pelo MMC, obteremos:

3 + (x+2)=0

cuja solução é x= -5

Exercícios: Resolver as equações do segundo grau fracionárias:

x + 6/x = -7
(x+2)/(x+1) = 2x/(x-4)
(2-x)/x + 1/x² = 3/x
(x+2)/(x-2) + (x-2)/(x+2) = 1

Equações bi-quadradas

São equações do 4o. grau na incógnita x, da forma geral:

a x4 + b x² + c = 0

Na verdade, esta é uma equação que pode ser escrita como uma equação do segundo grau através da substituição:

y = x²

para gerar

a y² + b y + c = 0

Aplicamos a fórmula quadrática para resolver esta última equação e obter as soluções y' e y" e o procedimento final deve ser mais cuidadoso, uma vez que

x² = y' ou x² = y"

e se y' ou y" for negativo, as soluções não existirão para x.

Exemplos:

Para resolver x4-13x²+36=0, tomamos y=x², para obter y²-13y+36=0, cujas raízes são y'=4 ou y"=9, assim:
x² = 4 ou x² = 9

o que garante que o conjunto solução é:

S = { 2, -2, 3, -3}
Para resolver x4-5x²-36=0, tomamos y=x², para obter y²-5y-36=0, cujas raízes são y'= -4 ou y"=9 e desse modo:
x² = -4 ou x² = 9

o que garante que o conjunto solução é:

S = {3, -3}
Se tomarmos y=x² na equação x4+13x²+36=0, obteremos y²+13y+36=0, cujas raízes são y'= -4 ou y"= -9 e dessa forma:
x² = -4 ou x² = -9

o que garante que o conjunto solução é vazio.

1 - Anote o problema. O primeiro passo é anotar o problema para que possa começar a visualizar a solução. Digamos que ele seja o seguinte: -4x + 7 = 15.

2 - Decida se usará soma ou subtração para isolar a variável. O próximo passo é achar uma forma de deixar "-4x" de um lado e as constantes (números inteiros) do outro. Para isso, terá que usar a "aditiva inversa" achando o oposto de +7, que é -7. Subtraia 7 de ambos os lados da equação para que o "+7" do mesmo lado da variável seja cancelado. É só escrever "-7" abaixo do 7 de um lado e do 15 do outro, para que a equação continue balanceada.Lembre-se da regra de ouro da álgebra. O que você fizer a um lado da equação deverá ser feito do outro para manter o equilíbrio. É por isso que se subtrai 7 do 15 também. Precisamos tirar 7 apenas uma vez de cada lado, por isso é que ele não é subtraído de -4x também.

3 - Some ou subtraia a constante a ambos os lados da equação. Isso completará o processo de isolar a variável. Subtrair 7 de +7 do lado esquerdo da equação não deixará nenhum termo constante do lado esquerdo. Subtraindo o mesmo número de +15, você terá 8 do lado direito da equação. Assim, a nova equação será -4x = 8.

-4x + 7 = 15 =
-4x = 8

4 - Elimine os coeficientes da variável usando divisão ou multiplicação. O coeficiente é o número ligado à variável. Nesse exemplo, ele é -4. Para removê-lo, será necessário dividir os dois lados da equação por -4.

Novamente, tudo o que for feito de um lado da equação deve ser feito do outro. É por isso que você verá ÷ -4 duas vezes.

5 - Resolva a variável. Para isso, divida o lado esquerdo da equação, -4x, por -4 para obter x. Divida o lado direito, 8, por -4 para obter -2. Portanto, x = -2. Você precisou de dois passos - subtração e divisão - para resolver essa equação.

MÉTODO 2

1 - Anote o problema. Este será: -2x - 3 = 4x - 15. Antes de prosseguir, veja se as duas variáveis são iguais. Nesse caso, "-2x" e "4x" têm a mesma variável, "x", por isso você pode prosseguir.

2- Mova as constantes para o lado direito da equação. Para isso, será necessário usar adição ou subtração para eliminar a constante do lado esquerdo. Ela é -3, então você terá que pegar seu oposto, +3, e somá-lo aos dois lados da equação.
- Fazer isso lhe dará (-2x -3) +3, ou -2x do lado esquerdo.
- Adicionar +3 ao lado direito da equação lhe dará (4x - 15) +3, ou 4x - 12.
- Dessa forma, (-2x -3) +3 = (4x -15) +3 = -2x = 4x -12
- A nova equação será -2x = 4x -12
3- Mova as variáveis para o lado esquerdo da equação. Para isso, você só terá que pegar o "oposto" de "4x", que é "-4x", e subtraí-lo de ambos os lados da equação. Do lado esquerdo, -2x - 4x = -6x, e do lado direito, (4x -12) -4x = -12, portanto a nova equação será -6x = -12.
- -2x - 4x = (4x - 12) - 4x = -6x = -12
4- Resolva a variável. Agora que simplificou a equação para -6x = -12, só precisa dividir ambos os lados por -6 para isolar a variável x, que agora está sendo multiplicada por -6. Do lado esquerdo da equação, -6x ÷ -6 = x, e do lado direito, -12 ÷ -6 = 2. Portanto, x = 2.
- -6x ÷ -6 = -12 ÷ -6
- x = 2